Framsticks

Simulation physique (du corps de la créature)

Les corps des créatures sont divisés en petits morceaux (aux extrémités des bâtonnets) qui sont les points matériaux "idéaux". C'est l'approche de " la méthode des éléments finis " : tous les points du corps matériel ne sont pas simulés – seulement un nombre déterminé de points, représentant de petits volumes du corps. Le simulateur calcule toutes les forces affectant ces points donnés : pesanteur, réaction élastique quand il est lié à d'autres points, réaction et frottement au sol en touchant le sol, etc...

Certaines suppositions dans notre modèle sont utilisées afin de réduire les calculs. C'est une méthode numérique plus simple mais plus rapide qui est utilisée. C'est pourquoi certains résultats ne sont pas exacts en traitant de grandes forces.

L'image de droite montre des exemples de forces calculées par le simulateur physique de Framsticks.

---

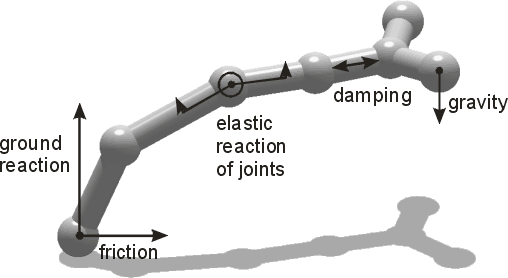Simulation du réseau de neurone (le cerveau de la créature)

Les neurones de Framsticks font une simple somme pondérées des signaux d'entrée. Les signaux d'entrée influence l'état du neurone, celui-ci ayant sa propre inertie. Des signaux forts changent l'état du neurone plus rapidement que des signaux faibles. La sortie du neurone est limitée à l'intervalle [ -1, +1 ] en utilisant une fonction sigmoïdale de base. On peut voir des exemples ci-dessous : ( entrée / état / sortie )

Excitation simple. L'état augmente quand l'entrée est positive et diminue quand l'entrée tend vers zéro. Notez que l'état d'un neurone peut descendre en dessous de zéro dû fait de son inertie.

Une courte mais forte impulsion donne des résultats semblables à un long mais faible signal.

Dans cet exemple, un signal fort cause la saturation du neurone (son état est très élevé). Les changements postérieurs de signal n'influenceront pas la sortie.

Les propriétés des neurones peuvent ętre changées par quelques éléments spéciaux du génotype à l'intérieur des descriptions des neurones. Chaque neurone a 3 paramètres :

• Force, signalé par '! ', intervalle de valeur : 0..1, la valeur de défaut vaut 0,04
  
• Inertie, signalé par ' = ', intervalle de valeur : 0..1, la valeur de défaut vaut 0,8
  
• Sigmoïde, signalé par ' / ', n'importe quel nombre, la valeur de défaut vaut 2,0
  

La force et l'inertie changent l'état interne du neurone. A chaque étape de simulation, l'état du neurone est modifié pars la valeur calculée à partir des excitations d'entrée. La force détermine la vitesse de changement de la valeur. La valeur maximum de 1,0 donne une réaction instantanée. Des valeurs basses, comme celle par défaut 0,04, charge et décharge doucement le neurone. L'inertie du neurone est semblable à l'inertie physique d'un corps : elle soutient sa tendance au changement d'état. Les valeurs basses d'inertie ont peu influence sur l'état. Les valeurs près du maximum (1,0) peuvent avoir comme conséquence des oscillations de l'état de neurone.

Exemples : ( entrée / état / sortie )

Force = 0.1, Inertie = 0 : Changement lent de l'état. Notez la réaction instantanée après l'impulsion de signal d'entrée quand l'inertie est désactivée.
Force = 0.1, Inertie = 0,8 : L'inertie étant activée, l'état du neurone augmente au-dessus de l'amplitude d'impulsion d'entrée, puis chute en dessous de zéro. L'état final tend vers zéro après plusieurs oscillations.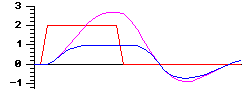
Force = 1, Inertie = 0 : Le coefficient maximum de force a comme conséquence une propagation de l'entrée vers la sortie d'une manière instantanée.

Le coefficient sigmoïdale change la fonction de sortie. Formules détaillées :

où :

input : somme pondérée des entrées du neurone,
velocity : analogue à la vitesse,
state : état interne (analogue à la position),
output : sortie.
L'abscisse représentant le temps.

Exemples :

Sigmoïde = 2.0 (défaut)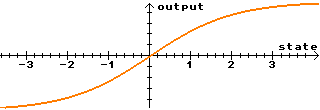
Sigmoïde = 10.0 (les valeurs élevées produisent presque une fonction de seuil)
Sigmoïde = 0.5 (les valeurs basses donnent presque une fonction de sortie linéaire)

---

Muscles et récepteurs

Un neurone avec une commande de muscle (' | ' ou ' @ ' dans le génotype du neurone) peut changer l'orientation relative du bâtonnet (par rapport au bâtonnet précédent). Une créature simple à 2 bâtonnets avec un muscle de flexion au milieu, est décrite par le génotype " XX[| ...] La jonction reste droite quand le signal est égal à 0. Les valeurs positives et négatives plient l'articulation dans les directions opposées.

	Le récepteur " G " (le gyroscope, équivalent au sens de l'équilibre) fournit les informations sur l'orientation du bâtonnet relativement à la force de pesanteur. Le gyroscope associé à un bâtonnet horizontal donne un signal valant 0 à sa sortie. La position verticale est perçue en tant que -1 ou +1 selon l'extrémité qui est la plus élevée.
	Le récepteur " T " (contact) peut ętre imaginé comme "une moustache de chat" fixé au bâtonnet. Son état détendu est -1 (rien n'est détecté dans l'intervalle des moustaches). La valeur du signal croît lorsque la moustache s'approche de n'importe quel objet matériel. Il atteint 0 quand le bâtonnet touche la terre. Des valeurs plus élevées signifient que le bâtonnet est poussé dans le sol.
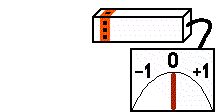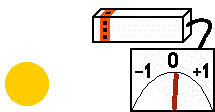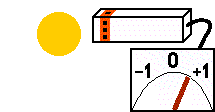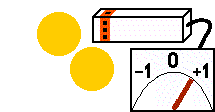	L'excitation du récepteur " S " (odorat) dépend de la somme des sources d'énergie voisines (des sphères d'énergie ou d'autres créatures). Le signal de sortie varie de 0 (rien n'est détecté) à 1 (maximum). Les sources d'énergie riches ou proches sont mieux détectées que les petites sources ou celles éloignées.